Types of vertical coordinates
Although each Feature has a Crs, the Crs tells only how to interpret the horizontal coordinates of the feature. So it is your own responsibility, as an application developer, to keep track of the unit and the meaning of the vertical coordinates (the z coordinates, or heights).
The unit is usually meter or foot.
The meaning is usually one of the following:
Height above mean sea level,
Height above a reference ellipsoid,
Height above ground,
Height above treetops.
The first one, height above mean sea level, is not a precisely defined notion. To be precise, one must specify the place and the period of time at which mean sea level was observed, and also the levelling network on land by which this sea level is propagated. This information specifies the location of the zero level surface, in other words the vertical datum. In addition, one must also specify the length unit and the direction of the vertical axis (heights are positive up, but depths are positive down). The result is a vertical coordinate reference system or vertical CRS; the term height system is also used.
Different nations use different vertical datums, just as they use different horizontal datums, but the good news is that when vertical datums are based on mean sea level, the mismatch between them is usually just a few meters or decimeters (unlike the mismatch between horizontal datums, which can be hundreds of meters).
With the arrival of satellite navigation, the Wgs84 reference ellipsoid has become an alternative way to specify the zero level of a vertical datum. Since the Earth is not quite homogeneous, the Wgs84 ellipsoid can differ from the mean sea level by up to about 110 meters.
The height above ground, or treetops, is usually not regarded as a kind of vertical datum, but it is a similar notion (although harder to define with high precision).
Most operators, including the ProjectOperator, does not modify the z coordinates of features. However, some operators do, for example:
The ElevationOperator can convert height above ground to height above sea level.
The OffsetOperator can offset heights by a fixed amount.
The UnitConversionOperator can convert heights between various length units.
The rest of this page gives more details about height systems and how to transform between them.
Height systems related to sea level
Traditionally, the mean sea level is the zero surface for heights, but the physical realization is often restricted to a particular country. The basis is a tide gauge, where the mean sea level has been observed over a long period (preferably 19 years) at a certain place. This level is then propagated over the entire country by spirit levelling, so that a large number of benchmarks with official heights are established. To determine the height at a new place, one must do more detailed levelling from the nearest official benchmarks.
The geoid is an idealization, defined to be the equipotential surface that best fits the mean sea level. In other words, we want the sea level to be undisturbed by systematic variations in wind, air pressure, water temperature and water salinity etc. - only the Earth gravity and rotation should affect the sea, and possibly the average tide effects of the moon and the sun. So in theory, there is only one geoid. However, there is not yet any international geoid realization, from which you can measure heights. There are plans for a World Height System with a consistency of a few centimeters, but it is still work in progress.
In practice, people have to use national height systems above "mean sea level", but they can differ from each other by up to a couple of meters, for many reasons:
A tide gauge does not measure the idealized sea level, but the actual mean sea level at a certain place. The effects of prevailing winds, currents, etc., will cause the actual mean sea level to differ from the idealized geoid. These variations are called ocean surface topography and can be up to 2 meters.
Some national height systems are not based on the observed mean sea level, but on observed low water or high water, and some are based on the level of the Caspian Sea (see Unusual Height Systems).
The technique to propagate heights over land by spirit levelling is quite accurate over short distances, but some errors can accumulate over long distances.
Spirit levelling across an entire country must be complemented with gravity measurements, otherwise the heights will not be consistent. But gravity can be measured only on the surface, and one would really need gravity measured underground as well. Instead, one has to make some assumptions about the density of the ground. There are basically two ways to make the assumptions: a) Either you do your best to estimate the density all the way down to the magma, and this will give you orthometric heights. There are various kinds of orthometric heights, depending on exactly how you estimate the density. b) Or you can make the simplest possible assumption about density - perhaps it should be called no assumption at all - and this will give you normal heights. The theoretical distinction between orthometric and normal height systems is difficult to understand, but the practical difference is small. Swiss authorities have used both approaches, based on the same measurements, and found differences up to 0.5 meters. Noel Zinn says that the differences, in general, can be up to 2 meters at high elevations. For normal heights, the zero-level surface is sometimes called a quasi-geoid. See Literature.
Height systems related to a reference ellipsoid
For detailed maps, the earth is usually modelled as an ellipsoid, since a sphere would be too inaccurate. But, although an ellipsoid is fine for horizontal positions and map projections, it will differ a lot from the sea level, vertically. For example, the WGS84 ellipsoid can differ up to 107 meters from sea level.
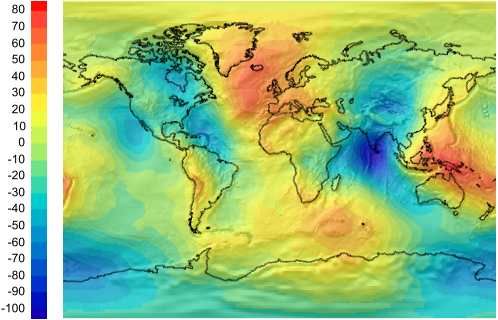 |
Before the satellite technology, local ellipsoids were used for national mapping. For example, the Bessel ellipsoid from 1841 has been used in many countries, but only the size and shape of the Bessel ellipsoid were the same. Each country gave the ellipsoid a slightly different position, so that it would fit their own part of the world. Although one can think about height above a local ellipsoid, such heights are not very useful, since there is no infrastructure to measure them directly. Meyer, Roman and Zilkoski say:
"In summary, local ellipsoids are essentially mathematical fictions that enable the conversion between geocentric, geodetic, and cartographic coordinate systems in a rigorous way and, thus, provide part of the foundation of horizontal geodetic datums, but nothing more. As reported by Fischer (2004), 'O’Keefe tried to explain to me that conventional geodesy used the ellipsoid only as a mathematical computation device, a set of tables to be consulted during processing, without the slightest thought of a third dimension.' " (See Literature.)
This changed with the satellite technology that gave us GPS and GLONASS, since it allows us to measure height above a global reference ellipsoid (WGS84 for GPS, PZ-90 for GLONASS). When a GPS receiver measures your height, it gets the height above the WGS84 ellipsoid. (But a modern receiver can use an internal geoid model to transform it to the height above sea level.)
Transformations between height systems
There are various ways to convert between height systems.
Sometimes, it is enough to use a vertical offset: you just add or subtract a constant term. For example, to transform a height expressed in New Zealand Vertical Datum 2009 to Dunedin 1958, you can add 49 cm (the 1 sigma accuracy will be 7 cm).
To get better accuracy, you can use vertical offset and slope, where the offset depends on horizontal position in a linear way. For example, you can transform a height from the Swiss LN02 to the European EVRF2007 like this: First express the horizontal position as n kilometers north and e kilometers east of the reference point 46° 55' N, 8° 11' E. Then, subtract
225 + 1.07 n + 0.16 e millimeters
from the LN02 height to get the EVRF2007 height. In Geneva in the southwest, you would subtract 117 mm, and in Kreuzlingen in the northeast, you would subtract 323 mm. (The 1 sigma accuracy of this transformation is 31 mm.)
However, the method with vertical offset, with or without slope, usually requires that the two height systems are of the same kind (above sea level or above an ellipsoid). Even then, such simple methods may not be accurate enough. A more accurate method is to use a raster, whose cells contains the height offsets. For each horizontal position, you can look up its height offset in the raster (using interpolation between nearby cell values). This method can of course represent as detailed a transformation as you would like. The cell size of the raster should usually be around 1 arc minute (1850 m) for high accuracy.
The only trouble is to find the rasters you need. They are usually published by the national Land Survey authorities.
One raster that is particularly useful is the EGM2008 geoid model, published by NGA, the US National Geospatial-Intelligence Agency. It is a quite detailed global model of the difference between mean sea level (the EGM2008 geoid) and the WGS84 ellipsoid. The vertical accuracy is estimated to be about 15 cm (RMS). So, when you want to transform to/from a national height system, but you cannot find a national geoid model, the EGM2008 model is usually a fairly good approximation. We believe the difference from a national model would usually be less than 1 or 2 meters, with some exceptions (see the next section).
The sample application Height Calculator Sample shows how you can transform heights by using raster data. The application uses a coarse raster for EGM2008 as well as rasters for two Swedish national height systems; the data are included in the Carmenta Engine Samples Geodata. The application uses the fact that all three rasters relate some geoid to the WGS84 ellipsoid, so that height above WGS84 ellipsoid can be used as a common denominator.
Sometimes, a geoid model refers to a nationally used ellipsoid. For example, the deprecated Swedish geoid model RN92 relates the RH70 geoid to the Bessel ellipsoid as it is located in the Swedish geodetic datum RT90. And in USA, a geoid model can refer to the NAD83 ellipsoid, which, although it has the same size and shape and the WGS84 ellipsoid, differs by about 2 meters in position (the ellipsoidal height can differ up to 1.65 m). This is seldom a problem in practice, though. If you need heights above an ellipsoid in USA, it is probably the NAD83 ellipsoid you should use anyway, since that ellipsoid is used for benchmark coordinates.
However, sometimes you do need to transform heights from one ellipsoid to another. This is often done with a 3-parameter or 7-parameter Helmert datum shift, but the HelmertDatumShift class in Carmenta Engine is designed not to change the z coordinate, so it cannot be used directly. (The reason is that GIS heights are usually above sea level, so transforming the z coordinate from ellipsoid to ellipsoid is seldom appropriate).
Instead, you can transform a height from ellipsoid to ellipsoid in three steps:
Convert your horizontal position and height above source ellipsoid into geocentric Cartesian coordinates [X, Y, Z]_S, by using the Crs.UnprojectToGeocentricXYZ method.
Compute geocentric Cartesian coordinates [X, Y, Z]_T in your target ellipsoid by using the Helmert formula, but use the linearized matrix of Burša-Wolf instead of Rz Ry Rx, for simplicity. See the HelmertDatumShift for the math, and contact Carmenta support if you get stuck.
Convert the result to horizontal position and height above target ellipsoid by using the Crs.ProjectFromGeocentricXYZ method.
Some unusual height systems
For some national height systems, EGM2008 would not be a very good approximation. Although we cannot account for the ocean surface topography here, we can warn you about some height systems that are not based on mean sea level. The offsets below are approximate and they refer to a "mean sea level" that is not well-defined, but the table gives a rough guide; the information comes from the EPSG database.
Vertical Datum | Area of Use | Offset from mean sea level |
|---|---|---|
AIOC 1995 (EPSG:5133) | Azerbaijan | -26.3 m |
Caspian Sea (EPSG:5106) | Caspian Sea | -28.0 m |
Hong Kong Chart Datum (EPSG:5136) | Hong Kong | -1.38 m |
Hong Kong Principal Datum (EPSG:5135) | Hong Kong | -1.23 m |
KOC Construction Datum (EPSG:5188) | Kuwait | -1.52 m |
KOC Well Datum (EPSG:5187) | Kuwait | +3.22 m |
Kuwait PWD (EPSG:5186) | Kuwait | -1.03 m |
Oostende (EPSG:5110) | Belgium | -2.32 m |
Poolbeg (EPSG:5152) | Ireland | -2.70 m |
For example, the zero level of Oostende was based on low water, and is about 2.32 meters below mean sea level. This means that for a point on the Belgian-Dutch border, the Belgians using Oostende would consider its height to be 2.32 meters greater than the Dutchmen would say. So, to transform a height above the WGS84 ellipsoid into an Oostende height, you may use the EGM2008 geoid model to get approximate height above mean sea level, but then you should add 2.32 meters.
Literature
Urs Marti, "Comparison of High Precision Geoid Models in Switzerland". In Dynamic Planet, International Association of Geodesy Symposia, 2007, Volume 130, Part III, pages 377-382.
Thomas H. Meyer, Daniel R. Roman, and David B. Zilkoski. "What does height really mean?" This is a series of four articles published in Surveying and Land Information Science, SaLIS.
Part I: Introduction, SaLIS Vol. 64, No. 4, pages 223-233, December 2004.
Part II: Physics and gravity, SaLIS Vol. 65, No. 1, pages 5-15, March 2005.
Part III: Height systems, SaLIS Vol. 66, No. 2, pages 149-160, June 2006.
Part IV: GPS heighting, SaLIS Vol. 66, No. 3, pages 165-183, September 2006.
Noel Zinn. "What's Up? Vertical and Tidal Datums." Presented at the monthly meeting of the Houston Chapter of the Hydrographic Society of America, July 2011.
Previous: Letting a DataSet read its CRS from data files
Up: Coordinate Systems: Contents