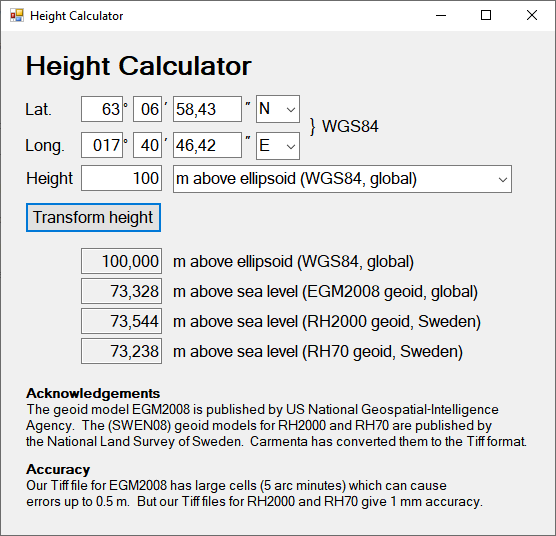
Height Calculator Sample
This page documents a sample application in the Carmenta Engine SDK, built using C# and Windows Forms. The purpose of the sample is to transform between height above the Wgs84 ellipsoid and height above mean sea level. To get some general background, see the article Types of vertical coordinates
We will not demonstrate how to recreate the sample step by step, but we will discuss some details.
 |
The method
The transformation method is to look up the horizontal position in a geoid model, implemented as a raster dataset, to get the local geoid height: the height of the geoid (the idealized mean sea level) above the Wgs84 ellipsoid. If we let N be the geoid height, H be a height above the geoid, and h be the corresponding height above the ellipsoid, then transformation between h and H can be done with the relation
h = H + N
The geoid models
However, "mean sea level" is not a well-defined notion if one requires high accuracy. So, the sample makes use of three different models of "mean sea level". Raster data for the models can be found in the Carmenta Engine Samples Geodata, which you must install before you can run the sample.
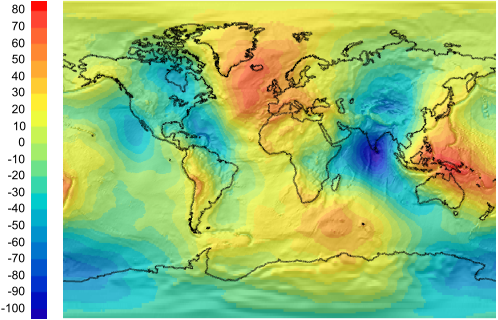
EGM2008: This is a global geoid model, developed by NGA (US National Geospatial-Intelligence Agency).
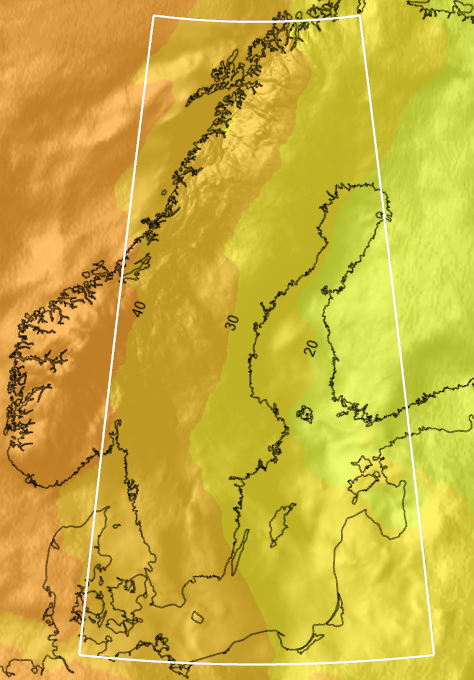
SWEN08_RH2000: This is the latest geoid model for the Swedish height system RH2000, published by the National Land Survey of Sweden.
SWEN08_RH70: This is the latest geoid model for the Swedish height system RH70, published by the National Land Survey of Sweden.
The Swedish models can be used only in Sweden (latitude 54° to 70° N, longitude 10° to 25° E).
The three models give slightly different results. Heights expressed in EGM2008 are usually 15 to 25 cm less than they are in RH2000. The difference between RH70 and RH2000 is more complex, partly because of lower quality in RH70, and partly because of glacial rebound: the ground near Umeå raised about 30 cm between the years 1970 and 2000.
All three geoid models have been published as raster data. Carmenta has converted them to compressed and tiled GeoTIFF files.
 |
 |
Choosing unit and offset
To save space, the raster values were converted to 16-bit signed integers, with a suitable length unit and offset to make good use of the 16-bit integer range.
For EGM2008, the geoid heights vary between -108 and +87 meters, and we chose the decimeter as the height unit, and no offset (the centimeter would also fit in the 16-bit integer range, but the decimeter gives better GeoTIFF compression).
For RH2000 and RH70, the geoid heights vary only between +17 and +44 meters. To get good accuracy, we chose the millimeter as the height unit. Then, to be able to fit all data in the range of 16-bit signed integers, we also chose the offset 30 meters. That is, the raster value 0 means 30.000 meters, the value 1 means 30.001 meters, etc.
In the case of the EGM2008 model, we did not convert to GeoTIFF directly from the NGA data; instead we started from EGM2008 representations published by Charles Karney as part of his GeographicLib.
There is a problem with using an offset and an unusual unit: they are easy forget. In our sample data, we used the possibility to store an Offset and a Scale as metadata in a GeoTIFF file. These metadata can be read by a GdalDataSet, which attaches them as numeric attributes to the raster features, and the Offset and Scale are also applied automatically by the method DataSet.GetNormalizedFloatValueAt(point). That is, when this method finds (or interpolates) the cell value c in a raster, it will return c * Scale + Offset. That's why you will not find any mention of the length units or the offset in the application code: it is taken care of behind the scenes.
Choosing raster resolution
For the Swedish geoid models, we chose the official resolution: 0.02 degrees in latitude and 0.04 degrees in longitude (about 2 km).
For EGM2008, we chose a resolution of 5 arc minutes (about 9 km), which is coarse but saves disk space.
Expected accuracy
For the Swedish geoid models, our sample uses the official resolution and the official interpolation technique (bilinear), so any error should be caused by our rounding the geoid heights to millimeters. So the maximal difference from the official values should be 0.5 mm.
Note that the Swedish geoid models themselves are not perfect; the Land Survey estimates that they have an RMS error about 10 to 15 mm compared to reality (worse offshore and in the highest mountains in the northwest).
For EGM2008, our implementation can deviate more from an official implementation, mainly due to our coarse resolution of 5 arc minutes. For this resolution, and with bilinear interpolation, Charles Karney has computed the maximal error for an EGM2008 representation to be 47.8 cm, and the RMS error to be 1.2 cm. However, Karney uses a vertical unit of 3 mm in his rasters. Since we have rounded the cell values to decimeters to improve file compression, our results can deviate from Karney's by up to 5 cm, so the maximal error in our application might be up to 53 cm (that's a quick worst-case bound). And we think our RMS error is about 3 or 4 cm.
Like the Swedish models, the EGM2008 itself is not a perfect model of reality. The goal for EGM2008 was an accuracy of 15 cm RMS worldwide, which seems to have been achieved.
When creating the GdalDataSet for each geoid model, it is important to set the Continuous property to True, otherwise Carmenta Engine will not interpolate when looking up geoid heights, and Nearest Neighbor would give worse accuracy.
Literature
US National Geospatial-Intelligence Agency. Earth Gravitational Model 2008 (EGM2008).
US National Geospatial-Intelligence Agency. Description of files containing propagated error estimates from EGM2008 on global 5’×5’ grids.
National Land Survey of Sweden. Svenska geoidmodeller (Swedish geoid models), retrieved 2023-03-28.
Jonas Ågren, Beskrivning av de nationella geoidmodellerna SWEN08_RH2000 och SWEN08_RH70 (Description of the Swedish geoid models SWEN08_RH2000 and SWEN08_RH70), LMV-Rapport 2009:1.
Charles Karney. GeographicLib: Geoid height.