HelmertDatumShift Class
A seven-parameter Helmert coordinate transformation from one GeodeticDatum to another.
NuGet/Assembly: Carmenta.Engine.5.17.0.nupkg (in the CECore assembly)
Syntax
public class HelmertDatumShift : DatumShiftRemarks
A HelmertDatumShift is the most commonly used kind of DatumShift. It has seven parameters that define a similarity transformation in 3D space. That is, each geographic object is transformed rigidly by parallel translations, rotations, and a scaling. This kind of coordinate transformation can model the systematic difference between two geodetic datums (a difference that is often hundreds of meters), but it cannot model smaller random differences caused by measurement errors (distortions). As a result, the accuracy of a Helmert datum shift can be as good as a few decimeters for a geodetic datum surveyed in the 1960s or later, like the Swedish RT90 or the Swiss CH1903+, but the accuracy may be several meters for older geodetic datums like the British OSGB1936. Also, the accuracy is usually better if the geodetic datum covers a small area, since errors of measurement will accumulate over larger areas.
When a Helmert datum shift transforms coordinates from its owner datum to its knownDatum, the longitude and latitude in the owner datum is first converted to 3-dimensional geocentric Cartesian coordinates, usually written X, Y, Z. The origin of this coordinate system is the center of the reference Ellipsoid, and the positive Z-axis goes through the North Pole, the positive X-axis goes through the equator at the PrimeMeridian (usually Greenwich), and the positive Y-axis goes through the equator at 90° east of the prime meridian. The point expressed in X, Y, Z coordinates is then rotated around each of the axes, by the angles RotationX, RotationY and RotationZ, and then scaled by the ScaleDifference, and finally parallel-translated by the offsets DX, DY and DZ. The resulting X, Y, Z coordinates in the knownDatum are eventually converted to longitude and latitude.
Traditionally, the input and output points should really be in 3D (long, lat, height), where the original height should be above the source ellipsoid and the output height should be above the target ellipsoid. However, Carmenta has noted that the z coordinates of GIS data are usually heights above sea level, which are best to leave undisturbed during a horizontal datum shift. So Carmenta Engine ends a Helmert datum shift by restoring the output height to the original height.
If you do need to transform heights, see Types of vertical coordinates
Formally, we have a defining formula:
The Helmert formula
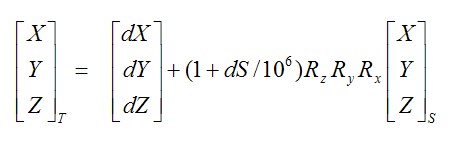 |
The point to the far right consists of geocentric coordinates X, Y, Z in S, a source geodetic datum. On the left hand side, the same point is expressed in T, a target geodetic datum. The dS is the value of scaleDifference (which is expressed in parts per million). And the matrices Rz, Ry, and Rx are rotation matrices specified by RotationZ, RotationY, and RotationX. The formula can of course be used to transform a point expressed in S to a point expressed in T; this is the forward direction. But the formula can also be used backwards.
A HelmertDatumShift can be attached when a new GeodeticDatum is defined, and gives a relation to its KnownDatum. If the Direction is ToKnownDatum, then the source datum S in the formula is the new datum, and the target datum T is the KnownDatum. If the Direction is FromKnownDatum, it is the other way around.
Unfortunately, the Helmert formula is not universally agreed. The worst problem is that there are two opposite sign conventions for the rotation angles. Carmenta Engine supports both; the choice is determined by the RotationSignConvention and affects the definition of the rotation matrices Rz, Ry, Rx. If the wrong convention is specified, the result can err by hundreds of meters.
The simplified Burša-Wolf formula
There are also other variants of the formula, which are more harmless. For example, the rotation matrices may be multiplied in a different order. In fact, many countries use a simpler linear matrix instead of the product Rz Ry Rx, and then, there is no multiplication order to define (since only one matrix is used). This variant is known as the Burša-Wolf formula. Depending on the rotation sign convention, the linear matrix would be either
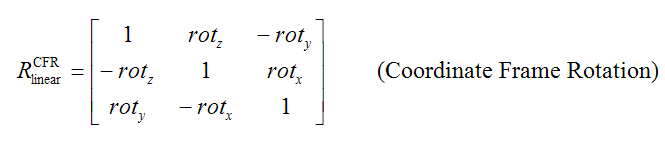 |
or
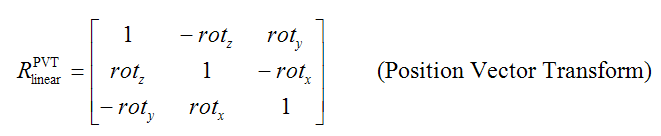 |
where the rotation angles must be expressed in radians. As long as the rotation sign convention is correct, the Burša-Wolf formula will usually differ by at most a few centimeters from the Helmert formula, since the rotation angles are usually small (less than 5 arc seconds).
Terminology
The Helmert datum shift is also known as a 3-D Helmert transform, or a 3-D conformal transform, or a 3-D similarity transform, or a 7-parameter transform, or a 3-parameter transform if only DX, DY and DZ are used.
The EPSG regards it as three different coordinate operation methods, namely "Position Vector 7-parameter transformation" (code 9606) or "Coordinate Frame Rotation" (code 9607), depending on the rotation sign convention, or else "Geocentric Translations" (code 9603) if only DX, DY and DZ are used. Formally, the EPSG methods uses the Burša-Wolf formula, but some of the instances in the EPSG database were originally published and intended for the Helmert formula.
According to some sources, the difference between Helmert and Burša-Wolf is not whether the rotation matrix is linearized (as described above), but is instead the sign convention for the rotation angles. But we think this is a misunderstanding, used only in a few texts.
Inheritance Hierarchy
System.Object
EngineObject
ResourceObject
DatumShift
HelmertDatumShift
Platforms
Windows, Linux, Android
HelmertDatumShift Members
The HelmertDatumShift type has the following members.
Constructors
| Name | Description |
|---|---|
| HelmertDatumShift | Initializes a new instance of the HelmertDatumShift class. |
Properties
| Name | Description |
|---|---|
| Authority | Gets the name of an authority, which is often "epsg". Inherited from DatumShift |
| AuthorityCode | Gets the unique code for the datum shift instance, according to the Authority, for example "15978". Inherited from DatumShift |
| Direction | Gets the direction: from or to the known datum. |
| DX | Gets the parallel translation along the X axis. |
| DY | Gets the parallel translation along the Y axis. |
| DZ | Gets the parallel translation along the Z axis. |
| Info | Gets documentation like accuracy and area of use. Inherited from DatumShift |
| IsDisposed | Gets a value that tells whether the current HelmertDatumShift has been disposed. Inherited from EngineObject |
| KnownDatum | Gets the known datum, usually WGS84. Inherited from DatumShift |
| Name | Gets or sets the name of the HelmertDatumShift. Inherited from ResourceObject |
| NativeHandle | Gets the native Carmenta Engine kernel object the current HelmertDatumShift represents. Inherited from EngineObject |
| RotationSignConvention | Gets the convention for the sign of rotations. |
| RotationX | Gets the rotation about the X axis. |
| RotationY | Gets the rotation about the Y axis. |
| RotationZ | Gets the rotation about the Z axis. |
| ScaleDifference | Gets the scale difference. |
| IUserProperties.UserProperties | Gets the AttributeSet that contains the user properties. Inherited from IUserProperties |
Methods
| Name | Description |
|---|---|
| Clone | Creates a copy of an object. Inherited from EngineObject |
| Dispose | Releases the reference to the native Carmenta Engine kernel instance the EngineObject represents. Inherited from EngineObject |
| Equals | Determines whether this instance is equal to another. Inherited from EngineObject |
| Constructs a datum shift from a DatumShiftInfo. Inherited from DatumShift |