LambertConformalConicProjection Class
A Lambert Conformal Conic Projection, with one or two standard parallels.
NuGet/Assembly: Carmenta.Engine.5.17.0.nupkg (in the CECore assembly)
Syntax
public class LambertConformalConicProjection : ProjectionRemarks
Johann Heinrich Lambert published his conformal conic map projection in 1772, but it was little used before the 1900s. It is conformal everywhere except at the poles. One pole will be shown as a point from which the meridians radiate as straight lines, equally spaced. But meridians that are 1° apart on Earth will be less than 1° apart in the projection. At the meridian that is antipodal to the centralLongitude, there will be an interruption: an unused sector of the map. The opposite pole is projected to a circle arc which is, in theory, infinitely far away. The projection is normally used for conformal mapping of areas that have larger extent west-east than north-south, like Russia. It is seldom used for very large scale maps, like city maps.
A sample map in Lambert Conformal Conic projection is shown in the picture.
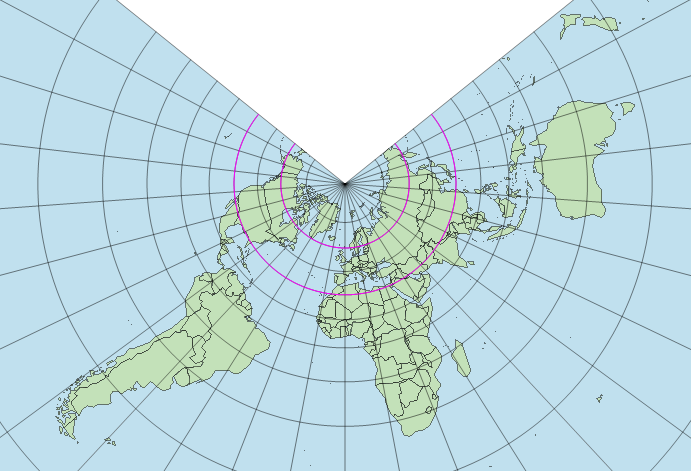 |
Traditionally, there are two different ways to construct a Lambert Conformal Conic, and we model this by two different constructors.
Lambert Conformal Conic (1SP): Give the latitude of minimal scale, and a scale factor. In the Carmenta Engine APIs, this is modelled by the constructor with seven arguments, where the centralLatitude argument specifies the latitude of minimal scale (and also the origin on the central meridian). In the Carmenta Studio, you must explicitly let both the StandardParallel1 and StandardParallel2 be equal to the centralLatitude.
Lambert Conformal Conic (2SP): Give the latitudes of two standard parallels, but no scale factor. A central latitude is also given, but it does not affect the shape of the map; it just specifies an arbitrary origin on the central meridian. In the Carmenta Engine APIs, this is modelled by the constructor with eight arguments. In the Carmenta Studio, you just let the ScaleFactor keep its default value of 1.
The name "1SP" ("one standard parallel") for the first construction method is widely used, but it is really an abuse of terminology if the scale factor differs from 1, because on a standard parallel, the nominal scale of a map should be true. And if the scale factor differs from 1, then the given central latitude (latitude of minimal scale) is not a standard parallel in this sense.
If we stick to the other, more common method "2SP", we can safely say that the nominal scale is true on the standard parallels, while geographic features appear too small between them, and too large outside them. There will be a latitude of minimal scale almost halfway between the two standard parallels. The image of a great circle will be concave when seen from this latitude. Near this latitude, a great circle will appear almost straight.
Extreme parameter values
When both standard parallels approach the same pole, the projection approaches a PolarStereographicProjection. In the other extreme, when both standard parallels - or just their average - approach the equator, the projection approaches a MercatorProjection. But the formulas for Lambert Conformal Conic break down when the limit is reached. Therefore, the average of the standard parallels must be at least one microdegree away from a pole and from the equator, otherwise an exception will be raised at construction. However, it is allowed (though unusual) to have StandardParallel1 and StandardParallel2 on opposite hemispheres.
Accuracy
The projection formulas use an ellipsoid model of the earth and have high accuracy. However, near the non-central pole, we use non-standard formulas to avoid huge or infinite projected coordinates. But if you take a projected point p near the non-central pole, and convert it to longitude/latitude and back again, the result is still equal to p. So, for internal use in Carmenta Engine, the effect is just that the projection is not conformal near the non-central pole. But if you want to export or import geodata as projected coordinates, you should not do so near the non-central pole (where the projection is very distorted anyway). The following table shows where the formulas are non-standard, assuming a projection intended for the northern hemisphere:
Lat. of smallest scale: | Non-standard formulas are used south of: |
|---|---|
50° N - 89.999° N | 80° S |
40° N - 50° N | 85° S |
30° N - 40° N | 88° S |
10° N - 30° N | 89° S |
0.001° N - 10° N | 89.98° S |
Inheritance Hierarchy
System.Object
EngineObject
ResourceObject
Projection
LambertConformalConicProjection
Platforms
Windows, Linux, Android
LambertConformalConicProjection Members
The LambertConformalConicProjection type has the following members.
Constructors
| Name | Description |
|---|---|
| LambertConformalConicProjection | Initializes a new instance of the LambertConformalConicProjection class. |
Properties
| Name | Description |
|---|---|
| Authority | Gets the name of an authority, which is often "epsg". Inherited from Projection |
| AuthorityCode | Gets the unique code for the projection instance, according to the Authority, for example "19883". Inherited from Projection |
| CentralLatitude | Gets the central latitude, also known as latitude of origin. |
| CentralLongitude | Gets the central longitude, also known as central meridian or longitude of origin. |
| FalseEasting | Gets the offset added to the projected x coordinates (the eastings). |
| FalseNorthing | Gets the offset added to the projected y coordinates (the northings). |
| IsDisposed | Gets a value that tells whether the current LambertConformalConicProjection has been disposed. Inherited from EngineObject |
| LengthUnit | Gets the length unit of the projected coordinates. |
| Gets a pre-defined LongLatProjection instance. Inherited from Projection | |
| Name | Gets or sets the name of the LambertConformalConicProjection. Inherited from ResourceObject |
| NativeHandle | Gets the native Carmenta Engine kernel object the current LambertConformalConicProjection represents. Inherited from EngineObject |
| ScaleFactor | A scale factor, by which all projected coordinates will be multiplied. |
| StandardParallel1 | Gets the first standard parallel. |
| StandardParallel2 | Gets the second standard parallel. |
| IUserProperties.UserProperties | Gets the AttributeSet that contains the user properties. Inherited from IUserProperties |
Methods
| Name | Description |
|---|---|
| Clone | Creates a copy of an object. Inherited from EngineObject |
| Dispose | Releases the reference to the native Carmenta Engine kernel instance the EngineObject represents. Inherited from EngineObject |
| Equals | Determines whether this instance is equal to another. Inherited from EngineObject |
| Returns one of the 120 predefined instances of Universal Transverse Mercator. Inherited from Projection |