Geographic Coordinates: Latitude and Longitude

Contents

• Introduction

• Plus or Minus

• Axis Order

• Angle Units

• Lat/Long Syntax

• The Lat/Long Graticule is not Unique: Geodetic Datums

Introduction

To make a global coordinate system for the Earth surface, we cover the Earth by a graticule (a latitude/longitude grid), where the horizontal lines are called parallel circles and have constant latitude, and the vertical lines are called meridians and have constant longitude.

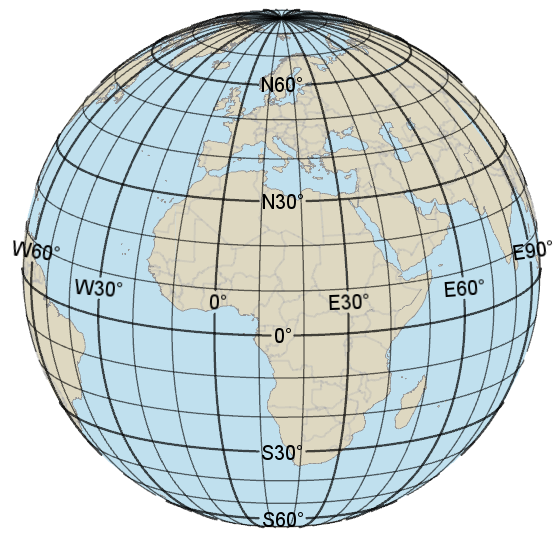The equator is the largest parallel circle and has latitude zero; the other parallel circles get a latitude that is their angular distance from the equator. So a valid latitude should be between 90° South and 90° North.

There is a so-called prime meridian with longitude zero; the other meridians get a longitude that is their angular distance from the prime meridian. So a valid longitude should be between 180° West and 180° East, although the range 0° to 360° East is sometimes used. Internationally, the prime meridian goes through Greenwich, London, but other prime meridians have been used locally.

Note that the parallel circles are separated by a constant distance, while the meridians meet at the poles. This means that a Lat/Long "square" of say 10 * 10 degrees is almost a true square near the equator, but nearer the poles it is more like a trapezoid.

Technically, the term geographic coordinates always mean latitude and longitude. Meter-based coordinates may be called map coordinates, but they are not geographic coordinates.

Plus or Minus

When latitude and longitude are represented as signed numbers, the most common convention is that latitudes are positive north of the equator and longitudes are positive east of Greenwich; this is how Carmenta Engine does it. However, Americans sometimes regard their longitudes west of Greenwich as being positive.

When latitude and longitude are written as text, it is more common to write an unsigned number together with an English abbreviation S, N, W or E, for South, North, West or East. The abbreviation can occur before or after the number, but ISO 6709 suggests after. Other languages than English have their own abbreviations:

Note that the abbreviation O can be ambiguous, as it means East in German and Swedish ("Ost"), but West in Spanish and French ("Oeste", "Ouest"). Therefore, the English abbreviations are often used in other languages, too.

On a printed map, both abbreviations and signs are often omitted, since they should be clear from context.

Axis Order

The usual convention of mathematicians (and GIS programmers) is that the right-axis coordinate is given before the up-axis coordinate, in other words longitude before latitude. This is how it works internally in Carmenta Engine: if you have a point expressed in Wgs84LongLat, then the X component is longitude and the Y component is latitude.

However, navigators and pilots traditionally use the opposite order, latitude before longitude, so this order should be used at least in a human interface.

Computer-to-computer protocols have often used the long/lat order, but the most recent standards of OGC (Open Geospatial Consortium) use the lat/long order. See also Axis order and axis names.

Angle Units

On maps of France and former French colonies, you may find latitude and longitude expressed in the angular unit gon (also known as grad) instead of degrees. A right angle = 90 degrees = 100 gon. One gon of latitude is approximately 100 km.

However, degrees are normally used. And one degree (1°) consists of 60 arc minutes (60'), and one arc minute consists of 60 arc seconds (60"). The reason to divide by 60 is just tradition.

Unfortunately, these units give us three distinct ways to describe an angle. As an example, let us take the Church of the Virgin Mary in Ystad:

The position of its tower can be described in the following ways:

• DDD.ddddd°   Decimal degrees may be most common in computer-based mapping systems, and are recommended by the international standard ISO 31-1, at least for angles in general.

• DDD° MM.mmm'   Degrees and decimal minutes are the maritime convention, the most common format in electronic navigation equipment, and are mandated by the NATO standard CJCSI 3900.01C.

• DDD° MM' SS.s"   Degrees, minutes and seconds are the most common format used to mark detailed maps. This format is suggested as a default format by ISO/FDIS 6709:2008, Annex D, in the absence of a user-community format.

Most GPS units can be configured to use any of these formats.

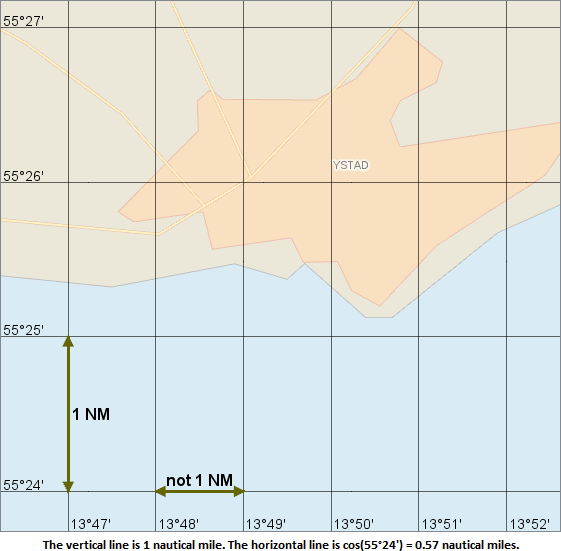
One degree of latitude is about 111 km. One degree of longitude is usually shorter, about 111 * cos(lat) km, since the meridians converge toward the poles. Similarly, one minute of latitude is about 1 nautical mile (1852 meters), while one minute of longitude is about cos(lat) nautical miles. And one second of latitude is about 31 m, while one second of longitude is about 31 * cos(lat) m.

Lat/Long Syntax

There is no unique standard syntax for the three formats. Since the degree character ° is hard to enter by keyboard (pro-tip for Windows: press and hold the Alt key while you type 0176 on the numeric keypad with NumLock on), some software accepts a lowercase d instead:

    55d 25.757' N      013d 49.117' E
    55d 25' 45.5" N    013d 49' 07.0" E

So a tolerant parser for this syntax should accept either a lowercase d or the proper degree character, and for good measure also the Unicode character masculine ordinal indicator since it can appear very similar to the degree character.

Furthermore, a printed book or a fancy website may not use the ASCII (typewriter) single quote and double quote for minutes and seconds, but the typographically correct Unicode characters prime and double prime, which usually appear more slanted. So a tolerant parser should accept either the ASCII single quote, the correct prime, or the incorrect but similar right single quotation mark for the minutes symbol, and accept either the ASCII double quote, the correct double prime or the incorrect but similar right double quotation mark for the seconds symbol.

There are also many other ways to write degrees, minutes and seconds. Instead of the unit symbols °, ' and " there can be one separator character, often a colon:

    55:25.757 N     013:49.117 E
    55:25:45.5 N    013:49:07.0 E

or a blank:

    55 25.757 N     013 49.117 E
    55 25 45.5 N    013 49 07.0 E

There is a NATO standard, CJCSI 3900.01C: "Position (point and area) reference procedures", that uses degrees and decimal minutes (four decimals) without any unit symbols or separators. So

    5525.7574N    01349.1166E

would stand for

    55° 25.7574' N    013° 49.1166' E

Although a latitude or longitude in this notation looks like a single decimal number, it is clear that it cannot be a number in decimal degrees (since the integer part is too large) or in meters (since the resolution would then be 0.1 millimeter).

Confusingly, people sometimes use degrees, minutes and decimal seconds expressed without unit symbols or separators, and with the decimal point of the seconds moved to be between the degrees and the minutes. So, for example,

    55° 25' 45.5" N    013° 49' 07.0" E

can be written as

    55.25455 N    013.49070 E

To ensure further confusion, a similarly moved decimal point is sometimes used for degrees and decimal minutes, so

    55° 25.757' N    013° 49.117' E

can be written as

    55.25757 N    013.49117 E

These two conventions are of course easily confused with each other, and with decimal degrees. Sometimes, the only clue is that when minutes and seconds are used, the first digit of a minute or second value must be in the range 0 to 5.

In general, it is good style to use a leading zero if a minute or second value is less than 10, so that the number always has two digits. Likewise, leading zeros should be used so that the integer part of latitude degrees has two digits, and the integer part of longitude degrees has three digits.

Finally, whether the decimal separator is a dot or a comma may depend on the numeric locale that is set on the computer operating system. However, some computer programs always require a decimal dot anyway, and other programs accept both a comma and a dot when reading, but will always write a dot.

In Carmenta Engine, there are some syntax-neutral methods in the Crs class that can help you parse and format degrees and decimal minutes or degrees, minutes and seconds. See for example Crs.ParseLatitude and Crs.FormatLatitudeAsDegreesMinutes.

The Lat/Long Graticule is not Unique: Geodetic Datums

A complication with geographic coordinates is that the lat/long graticule is not unique. An accurate global graticule was not possible to implement before satellite technology, so the tradition was that each country defined its own graticule, starting from a national origin point that was usually an observatory. The observatory determined its position in longitude and latitude by astronomical methods, and those methods gave an uncertainty of a couple of hundred meters. Then, the local graticule was extended countrywide by ground-based surveying methods that had much better accuracy, but not perfect.

The result is that we have hundreds of old national lat/long graticules, and some dozen continental ones, that can differ by hundreds of meters. The differences have four basic causes:

• an overall offset caused by the astronomical methods for locating the origin,

• an overall rotation caused by inaccurate determination of true north at the origin,

• an overall scale difference caused by an error when measuring a base distance,

• smooth but irregular distortions caused by accumulated errors in the ground-based surveying.

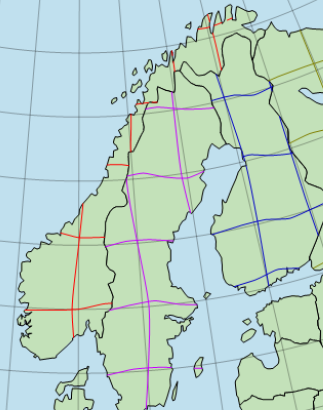These different graticules are usually known as geodetic datums, or sometimes terrestrial reference systems or terrestrial reference frames. The Carmenta Engine class is GeodeticDatum.

Nowadays, most countries have introduced modern geodetic datums more compatible with the global datum WGS84, and use of old-fashioned datums is discouraged. But the transition process is often slow, with the old and new datum being used in parallel for decades.

You may wonder: why are the modern datums only "more compatible" with WGS84 – why not simply use WGS84? The answer is continental drift. WGS84 is not attached to any solid ground, instead it is maintained to keep the average movement of all tectonic plates at zero, so the WGS84 coordinates of houses etc. are slowly changing over time as the tectonic plates are moving.

In Europe, for example, detailed mapping would often use the modern European datum ETRS89 which is plate-fixed: it is attached to the stable part of the Eurasian tectonic plate. By design, ETRS89 agreed with WGS84 on January 1, 1989, but the European ground is drifting by about 2.5 cm/year; in Sweden, the difference between ETRS89 and WGS84 is about 0.8 meters as of 2021.

Australia is on a tectonic plate that moves faster: the modern Australian datum GDA94 was designed to agree with WGS84 on January 1, 1994, but in 2020, the continent had moved about 1.8 meters toward north-northeast, and a new Australian datum GDA2020 was introduced, designed to agree with WGS84 on January 1, 2020.

Although Australia moves fast for a continent, it is on a single tectonic plate so it does not change its shape much. Unfortunately, some other countries have a less rigid shape. One effect of the catastrophic Tōhoku earthquake in 2011 was that parts of northeastern Japan suddenly moved up to 2.4 meters toward North America, and the Japanese geodetic datum JGD2000 had to be replaced by JGD2011.

By default, Carmenta Engine will treat most modern geodetic datums as equivalent to WGS84, since this is a great simplification and most Engine users can tolerate a position error of 1 or 2 meters; there are also situations where the errors will be much smaller, depending on the type of coordinate calculations. If you develop an application that needs very high accuracy, you can use other coordinate transformations than the default ones, or you can demand that all input coordinates are expressed in a single plate-fixed datum like ETRS89: for example, a sophisticated GPS receiver in Europe should be able to give its position in ETRS89 coordinates instead of WGS84.

A great introduction to geodetic datums can be found in the Guide to coordinate systems in Great Britain, published by the British Ordnance Survey.

Up: Coordinate Systems: Contents
Next: Projected Coordinates

Reference

GridGenerator

GeodeticDatum

Crs.ParseLatitude

Crs.ParseLongitude

Crs.FormatLatitudeAsDegreesMinutes

Crs.FormatLongitudeAsDegreesMinutes

Crs.FormatLatitudeAsDegreesMinutesSeconds

Crs.FormatLongitudeAsDegreesMinutesSeconds