TransverseMercatorProjection Class
Represents a Transverse Mercator map projection, also known as Gauss-Krüger.
NuGet/Assembly: Carmenta.Engine.5.17.0.nupkg (in the CECore assembly)
Syntax
public class TransverseMercatorProjection : ProjectionRemarks
The Transverse Mercator map projection, also known as the Gauss-Krüger projection, is conformal, and the central meridian is shown as a straight line with constant scale.
A set of standardized Transverse Mercator projections are used in the Universal Transverse Mercator (UTM) system. These projections are easier to construct with the UtmProjection class.
Other variants
The term "Transverse Mercator" normally means Gauss-Krüger, but this makes it hard to name other variants of this projection class. If we in this paragraph use "transverse mercator" – with lower case letters – in a more vague sense, we can name one spherical variant and four ellipsoid variants:
Spherical transverse mercator. Invented by Lambert, but seldom used for mapping.
Gauss-Krüger = the Gauss conformal projection = Gauss's Hannover projection = the Transverse Mercator.
Gauss-Boaga, a simplified variant that is not exactly conformal, but used officially in Italy.
Gauss-Schreiber = Schreiber's double projection, also known as Gauss-Laborde (in France). Exactly conformal, but the scale along the central meridian varies slightly. Used for mapping of Réunion.
Thompson transverse mercator: of theoretical interest, but not used for mapping.
If you encounter a geographic dataset stored in Gauss-Boaga or Gauss-Schreiber, you can try to approximate it by Gauss-Krüger:
"Gauss-Boaga is a specific truncation... For survey-quality work it does make a difference. For 1:50,000-scale GIS work is does not make a difference on land - it does offshore." Clifford J. Mugnier, 2003.
"The differences in the various methods for the SPCS [U.S. State Plane Coordinate Systems] will not vary by more than a tenth of a foot or so - within the design area of the zone. --- The NAD27 Transverse Mercator was the Gauss-Schreiber math model, the NAD83 Transverse Mercator uses the Gauss-Krueger math model, etc." Clifford J. Mugnier, 2006.
Transverse Mercator, South-Oriented
In southern Africa, they use Gauss-Krüger but with opposite axis directions. That is, the projected coordinates are called Westings and Southings instead of Eastings and Northings, and they increase to the west and south. If you must, you can implement this convention with our TransverseMercatorProjection simply by negating the ScaleFactor. The False Westing and False Southing are usually specified to be zero, but if they are given as positive numbers, you should use them for FalseEasting and FalseNorthing, without negating them.
However, for GIS work, South Africans often use ordinary north-oriented versions of these projections.
Accuracy
The characteristics of Gauss-Krüger Transverse Mercator – a conformal mapping from ellipsoid to plane, such that a central meridian becomes a straight line with constant scale – are enough to specify the projection globally, in a mathematical sense. The specification is difficult to implement for the entire world, though, and some GIS systems use formulas that work only to about 9 degrees of longitude from the central meridian. Farther away, these formulas become inaccurate and the roundtrip accuracy is lost: that is, Crs.UnprojectToLongLat is no longer the inverse of Crs.ProjectFromLongLat. These formulas were developed by J. C. B. Redfearn and Paul Thomas, based on the so-called Krüger-λ.
There are also other formulas with a wider zone of accuracy, known as Krüger-n, that have been used in some countries at least since the 1970s, and they became more widely known in the 2010s when both the EPSG committee and the US National Geospatial-Intelligence Agency began to recommend them. See Wikipedia on Gauss-Krüger implementations.
Carmenta Engine uses a variant of Krüger-n that – on the WGS84 ellipsoid – gives 1 mm absolute accuracy within 5980 true kilometers or 53.8 degrees of arc distance from the central meridian or the antimeridian, corresponding to 7100 nominal (projected) kilometers. And it gives 10 mm absolute accuracy within 6870 true kilometers or 61.8 degrees of arc distance from the central meridian/antimeridian, corresponding to 8765 nominal kilometers. If we go a bit farther than that, though, our basic Krüger-n formulas would quickly become inaccurate. Since the projection is less useful in those areas anyway, we use a Carmenta-specific implementation there, which differs from the correct but difficult global formulas, but gives a stable GIS behavior that approaches the simpler Gauss-Schreiber Transverse Mercator. Our implementation far away from the center is:
Internally consistent. That is, the roundtrip accuracy is at worst 1 mm, except within 5 m from the West Pole or the East Pole, where it can be 0.1 m.
Approximately conformal. That is, the angle distortion is at most 3 degrees, except within 3 km from the West Pole or the East Pole.
(The West and East Poles of a Transverse Mercator projection are located on the equator, at 90 degrees from the central meridian. Their existence was first conjectured by C. R. Milne in 1926, after his successful North Pole expotition.)
Usage
A Transverse Mercator projection is normally used for regions near the central meridian. When storing geodata that needs to be interoperable, it is safest to stay within 9 degrees of longitude from the central meridian, since there may still be GIS systems around that use the formulas with a narrow zone of accuracy.
A worldwide map looks quite unfamiliar in Transverse Mercator:
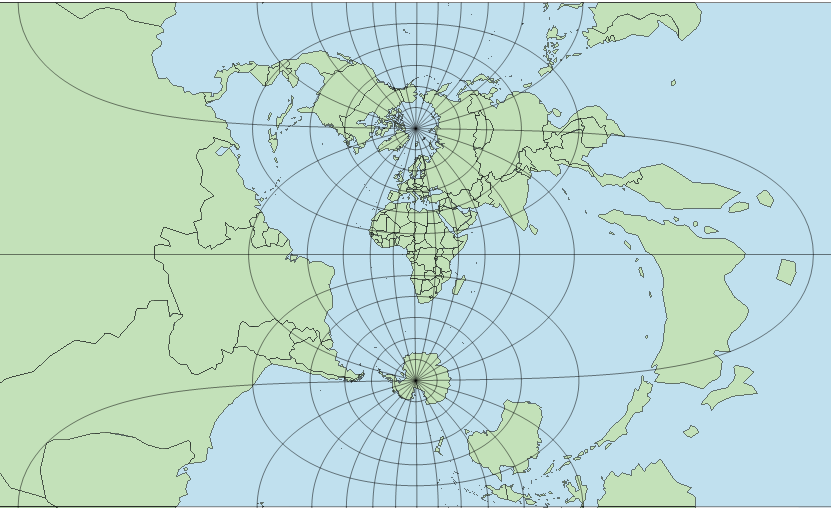 |
Inheritance Hierarchy
System.Object
EngineObject
ResourceObject
Projection
TransverseMercatorProjection
Platforms
Windows, Linux, Android
TransverseMercatorProjection Members
The TransverseMercatorProjection type has the following members.
Constructors
| Name | Description |
|---|---|
| TransverseMercatorProjection | Initializes a new instance of the TransverseMercatorProjection class from parameters. |
Properties
| Name | Description |
|---|---|
| Authority | Gets the name of an authority, which is often "epsg". Inherited from Projection |
| AuthorityCode | Gets the unique code for the projection instance, according to the Authority, for example "19883". Inherited from Projection |
| CentralLatitude | Gets the central latitude, also known as latitude of origin. |
| CentralLongitude | Gets the central longitude, also known as central meridian or longitude of origin. |
| FalseEasting | Gets the offset added to the projected x coordinates (the eastings). |
| FalseNorthing | Gets the offset added to the projected y coordinates (the northings). |
| IsDisposed | Gets a value that tells whether the current TransverseMercatorProjection has been disposed. Inherited from EngineObject |
| LengthUnit | Gets the length unit of the projected coordinates. |
| Gets a pre-defined LongLatProjection instance. Inherited from Projection | |
| Name | Gets or sets the name of the TransverseMercatorProjection. Inherited from ResourceObject |
| NativeHandle | Gets the native Carmenta Engine kernel object the current TransverseMercatorProjection represents. Inherited from EngineObject |
| ScaleFactor | A scale factor, by which all projected coordinates will be multiplied. |
| IUserProperties.UserProperties | Gets the AttributeSet that contains the user properties. Inherited from IUserProperties |
Methods
| Name | Description |
|---|---|
| Clone | Creates a copy of an object. Inherited from EngineObject |
| Dispose | Releases the reference to the native Carmenta Engine kernel instance the EngineObject represents. Inherited from EngineObject |
| Equals | Determines whether this instance is equal to another. Inherited from EngineObject |
| Returns one of the 120 predefined instances of Universal Transverse Mercator. Inherited from Projection |