EllipseOperator.Radius Property
Gets or sets the length of one semi-axis in the ellipse.
Syntax
public AttributeVariable< System.Double > Radius { get; set; }Property Value
Default: 10.0
The length of one semi-axis in the ellipse, in the length unit specified by RadiusUnit.
Remarks
When the Ratio is 1, a circle will be generated with the given Radius.
When the Ratio differs from 1, an ellipse will be generated. The semi-axis that goes in the given Direction from center will get length Radius, and the other semi-axis will get length Radius * Ratio.
If the Radius for an incoming point evaluates to 0.0 exactly, then no ellipse will be generated around that point.
Note that you may need to increase the Margin to ensure that it is larger than the longest possible radius.
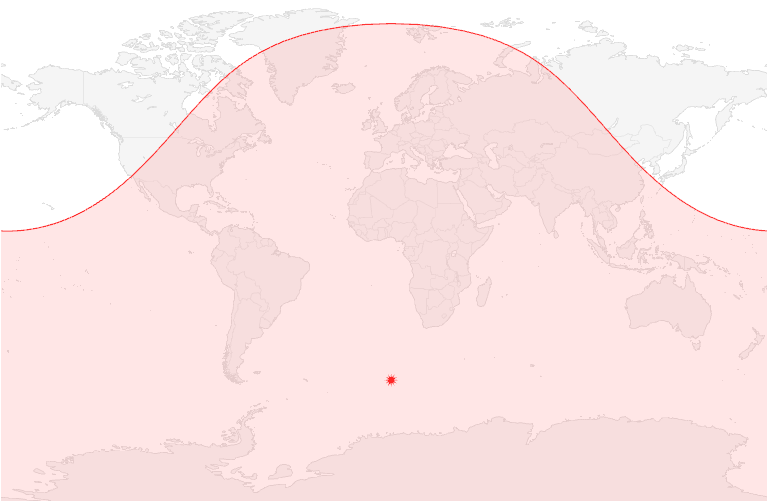
Displaying a circle larger than half the world
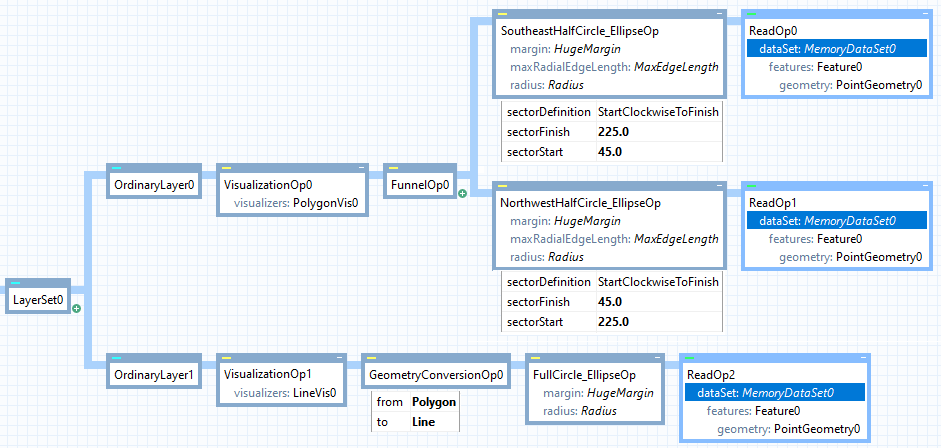
Provided that the Margin is large enough, the operator can handle very large values of Radius. However, if the radius is longer than 10 000 km or 90 degrees of arc distance, then the inside area of the generated polygon can become larger than the outside area, which can confuse the reprojection mechanism of Carmenta Engine, and in the map window, it may be the smaller outside that is filled with the polygon fill color. But there is a workaround that allows you to display such a large circle properly via two layers.
One layer generates the large circle with an EllipseOperator in the straightforward way, but uses only a LineVisualizer. It can be useful to convert the output polygon to a line via a GeometryConversionOperator.
The other layer uses only a PolygonVisualizer, and it uses a FunnelOperator reading from two parallel EllipseOperator instances that generates one half-circle each; in this way, each half-circle will cover less than half the world. Also, these two ellipse operators need a user-defined MaxRadialEdgeLength value, let us say 500 km. We have found that an oblique division between the half-circles works best, as in the configuration below.
 |
 |
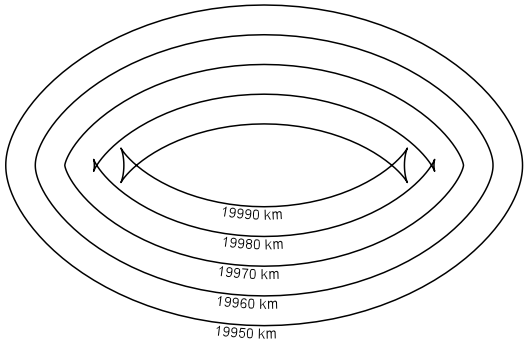
A curious effect is that if the circle radius is nearly 180 degrees of arc distance, or more precisely, longer than 19 970 326 m = pi * a * (1 − f ) where a is the equatorial radius and f is the flattening of the WGS84 ellipsoid, then the contour of the generated circle can intersect itself. This is caused by the ellipsoid being flattened at the poles: a radial path that goes near a pole has a shorter distance to the antipode than one that doesn't.
 |
Platforms
Windows, Linux, Android