DensityQuery.Blur Property
Gets or sets the bandwidth (standard deviation) of the smoothing kernel.
Syntax
public System.Double Blur { get; set; }Property Value
Default: 2.0
The bandwidth (standard deviation) of the smoothing kernel.
Remarks
When a DensityDataSet is queried, it will first compute the naive density value for each raster cell (as in a 2D histogram), and these values are then smoothed by a Gaussian or normal kernel function. The Blur distance gives the standard deviation of the kernel: in other words, it determines how much the contributions from each point feature shall be smoothed out.
Since the Gaussian kernel is a function that never quite reaches zero, the contributions from each point feature should in theory extend infinitely far away, but that would be inefficient to compute, and the conventional wisdom is that contributions beyond three standard deviations are very small and can be ignored. But the number 3 is somewhat arbitrary, and we have seen some examples where a larger value improves the results, so this is parameterized by the CroppingFactor, with default = 3.
As an example, let us assume that we have an isolated point feature, and that the cell size of the output raster is 84.67 meters (as determined by the ResolutionFactor and the view scale).
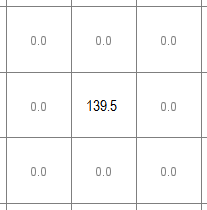
If we had used a zero Blur, we would get no smoothing, and the density value of the raster cell that contains the point feature would be 1 / (84.67 * 84.67) = 0.0001395 points per square meter, which is converted to 139.5 points per square kilometer. The neighboring raster cells would contain a density value of zero, since they contain no points.
 |
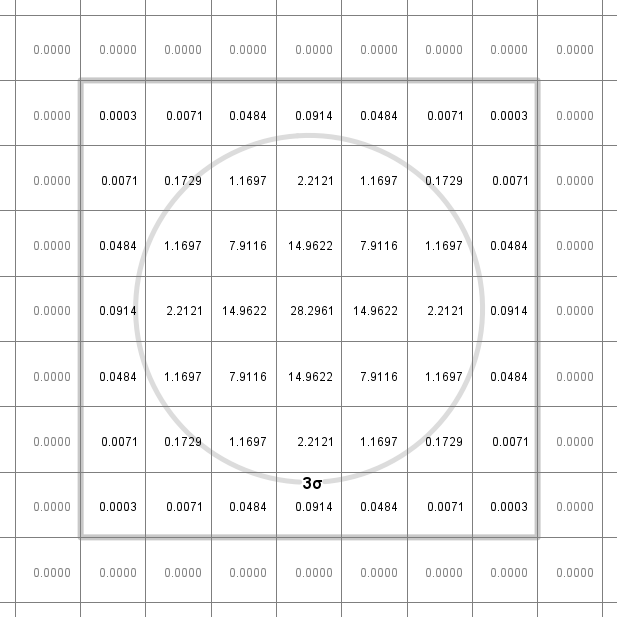
Now, let us suppose we want to smooth the density value 139.5 over many raster cells. We can use a Blur or standard deviation (sigma) of 75 meters, say. With the default CroppingFactor of 3, we get a cropping radius of 3 * 75 = 225 meters, and the circle with that radius is shown below. The three sigma circle is extended outward to become a square aligned with the raster cell borders, and the contributions from the central point feature are cropped to the interior of this square. The sum of the smoothed numbers is 139.5.
 |
Platforms
Windows, Linux, Android