Crs.IntersectLineSegments Methods
Returns the points where two line segment intersect.
Overload List
| Name | Description | |
|---|---|---|
| Public method | IntersectLineSegments(PointCollection line1, LineType line1Type, PointCollection line2, LineType line2Type) | Returns the points where two line segment intersect. |
| Public method | IntersectLineSegments(Point line1Start, Point line1End, LineType line1Type, Point line2Start, Point line2End, LineType line2Type) | Returns the points where two line segment intersect. |
| Public method | IntersectLineSegments(IEnumerable< Point > line1, LineType line1Type, IEnumerable< Point > line2, LineType line2Type) | Returns the points where two line segment intersect. |
IntersectLineSegments(PointCollection line1, LineType line1Type, PointCollection line2, LineType line2Type)
Returns the points where two line segment intersect.Syntax
public PointCollection IntersectLineSegments (
PointCollection line1,
LineType line1Type,
PointCollection line2,
LineType line2Type
)Parameters
The first line segment, represented as a collection of exactly two points.
The second line segment, represented as a collection of exactly two points.
Return Value
A collection of the points where the two line segment intersects.
Remarks
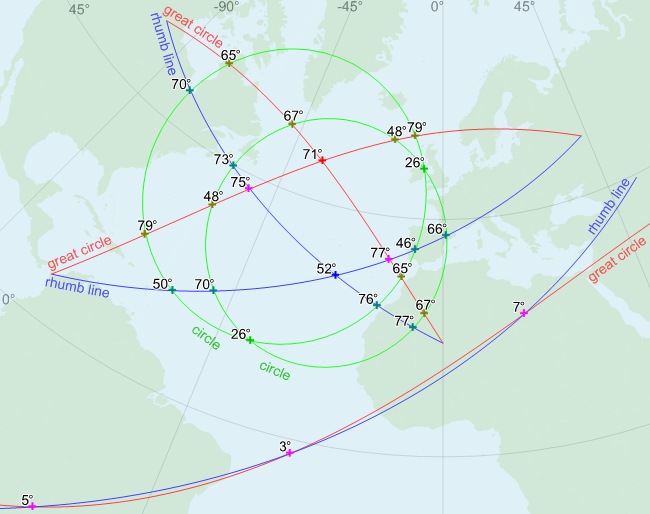
Two lines are given, each with exactly two points, together with their types (GreatCircle or RhumbLine). The returned list of points will contain the points where the lines intersect. If the lines are of the same type, they can intersect at most once. However, a great circle can intersect a rhumb line up to three times (even if the segments are short); see the map below.
Line type and accuracy
The possible line types are GreatCircle and RhumbLine (the GreatCircleApprox is not implemented). However, if the projection is non-georeferenced, then the line segments are regarded as a straight lines in the plane, giving unknown accuracy on Earth. Otherwise, the line segments are unprojected to LongLat, then the intersections are computed in LongLat, and they are finally projected. Disregarding the errors that may be caused by UnprojectToLongLat and ProjectFromLongLat, the intersections are found with submillimeter accuracy. However, before the calculations are done, both line segments are extended by 1 millimeter at both ends. This should ensure that the method will not overlook a valid intersection that is very close to one end of an original segment, although it may report a spurious intersection that really occurs slightly beyond one end of an original segment. This slight overreporting of intersections is usually better than possibly overlooking a valid intersection.
Intersection angle and error propagation
The z value of each intersection point does not mean altitude: it is the angle of intersection in degrees, in the range 0° to 90°. A small intersection angle means that small errors in the input coordinates can cause large errors in the intersection points. If the input coordinates may have an error err, then a point where the lines intersect with the angle alpha may have an error of err/tan(alpha/2). For example, if err is 1 meter and the alpha is 5°, then the intersection point may have an error of 1/tan(2.5°) = 23 meters.
 |
IntersectLineSegments(Point line1Start, Point line1End, LineType line1Type, Point line2Start, Point line2End, LineType line2Type)
Returns the points where two line segment intersect.Syntax
public PointCollection IntersectLineSegments (
Point line1Start,
Point line1End,
LineType line1Type,
Point line2Start,
Point line2End,
LineType line2Type
)Parameters
The start of the first line segment.
The end of the first line segment.
The start of the second line segment.
The end of the second line segment.
Return Value
A collection of the points where the two line segment intersects.
Remarks
Two lines are given, each with exactly two points, together with their types (GreatCircle or RhumbLine). The returned list of points will contain the points where the lines intersect. If the lines are of the same type, they can intersect at most once. However, a great circle can intersect a rhumb line up to three times (even if the segments are short); see the map below.
Line type and accuracy
The possible line types are GreatCircle and RhumbLine (the GreatCircleApprox is not implemented). However, if the projection is non-georeferenced, then the line segments are regarded as a straight lines in the plane, giving unknown accuracy on Earth. Otherwise, the line segments are unprojected to LongLat, then the intersections are computed in LongLat, and they are finally projected. Disregarding the errors that may be caused by UnprojectToLongLat and ProjectFromLongLat, the intersections are found with submillimeter accuracy. However, before the calculations are done, both line segments are extended by 1 millimeter at both ends. This should ensure that the method will not overlook a valid intersection that is very close to one end of an original segment, although it may report a spurious intersection that really occurs slightly beyond one end of an original segment. This slight overreporting of intersections is usually better than possibly overlooking a valid intersection.
Intersection angle and error propagation
The z value of each intersection point does not mean altitude: it is the angle of intersection in degrees, in the range 0° to 90°. A small intersection angle means that small errors in the input coordinates can cause large errors in the intersection points. If the input coordinates may have an error err, then a point where the lines intersect with the angle alpha may have an error of err/tan(alpha/2). For example, if err is 1 meter and the alpha is 5°, then the intersection point may have an error of 1/tan(2.5°) = 23 meters.
 |
IntersectLineSegments(IEnumerable< Point > line1, LineType line1Type, IEnumerable< Point > line2, LineType line2Type)
Returns the points where two line segment intersect.Syntax
public PointCollection IntersectLineSegments (
IEnumerable< Point > line1,
LineType line1Type,
IEnumerable< Point > line2,
LineType line2Type
)Parameters
The first line segment, represented as a collection of exactly two points.
The second line segment, represented as a collection of exactly two points.
Return Value
A collection of the points where the two line segment intersects.
Remarks
Two lines are given, each with exactly two points, together with their types (GreatCircle or RhumbLine). The returned list of points will contain the points where the lines intersect. If the lines are of the same type, they can intersect at most once. However, a great circle can intersect a rhumb line up to three times (even if the segments are short); see the map below.
Line type and accuracy
The possible line types are GreatCircle and RhumbLine (the GreatCircleApprox is not implemented). However, if the projection is non-georeferenced, then the line segments are regarded as a straight lines in the plane, giving unknown accuracy on Earth. Otherwise, the line segments are unprojected to LongLat, then the intersections are computed in LongLat, and they are finally projected. Disregarding the errors that may be caused by UnprojectToLongLat and ProjectFromLongLat, the intersections are found with submillimeter accuracy. However, before the calculations are done, both line segments are extended by 1 millimeter at both ends. This should ensure that the method will not overlook a valid intersection that is very close to one end of an original segment, although it may report a spurious intersection that really occurs slightly beyond one end of an original segment. This slight overreporting of intersections is usually better than possibly overlooking a valid intersection.
Intersection angle and error propagation
The z value of each intersection point does not mean altitude: it is the angle of intersection in degrees, in the range 0° to 90°. A small intersection angle means that small errors in the input coordinates can cause large errors in the intersection points. If the input coordinates may have an error err, then a point where the lines intersect with the angle alpha may have an error of err/tan(alpha/2). For example, if err is 1 meter and the alpha is 5°, then the intersection point may have an error of 1/tan(2.5°) = 23 meters.
 |
Platforms
Windows, Linux, Android