Crs.AngleFromAzimuth Method
AngleFromAzimuth(Point point, System.Double azimuth)
Computes grid azimuth from true azimuth.Syntax
public System.Double AngleFromAzimuth (
Point point,
System.Double azimuth
)Parameters
A point expressed in the Crs.
A true azimuth from the point, in degrees clockwise from true north.
Return Value
The grid azimuth, in degrees clockwise from grid north.
Remarks
Converts a true azimuth at a point in the coordinate reference system (from north clockwise in degrees) to an angle (grid azimuth, from grid north clockwise in degrees).
The only projections, for which the returned angle always equals the azimuth, are MercatorProjection using ellipsoid formulas (this is one reason why Mercator is popular for navigation) and NonGeoreferencedProjection (when the Crs is not georeferenced, saying "angle = azimuth" is simply the best guess that can be made).
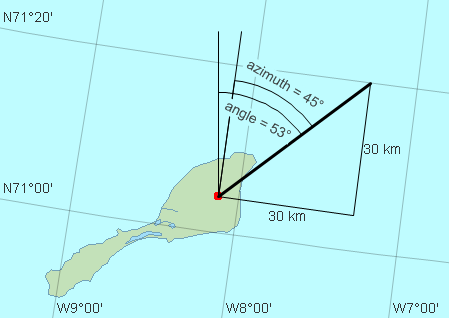
For conformal projections in general, there is at each point a constant difference between the azimuth and the angle. For example, in UPS North, the angle from up at Beerenberg, Jan Mayen, is always 8.1° greater than the azimuth. See picture below.
 |
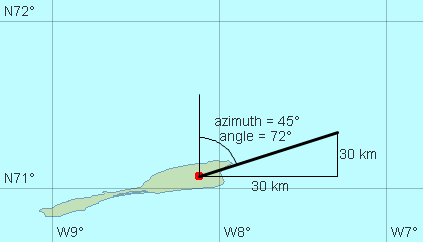
For non-conformal projections, the difference between azimuth and angle is usually not constant at a point. For example, if the projection is a regular cylindrical one (like Projection.LongLat or MillerCylindricalProjection), north is always up and east is always right (so that the returned angle will equal the azimuth if azimuth is 0°, 90°, 180° or 270°). However, northeast (azimuth 45°) is not always angle 45° from up: in LongLat, the west-east scale at Jan Mayen is 3 times larger than the north-south one, which causes azimuth = 45° to correspond to angle = 72°. See picture below.
 |
Troublesome input
The input can be troublesome in two ways:
The point p can be at or very near a pole. The trouble is that from the north pole, all geographic directions go south (have azimuth = 180°), and from the south pole, all geographic directions go north (have azimuth = 0°).
The point p can be outside the projection boundary (outside the world map according to this Crs). The problem is of course that the true north direction is not defined there.
The result for a troublesome point p depends on the projection type, but often the method just returns the input azimuth unchanged. An exception should never be thrown by this method.
Accuracy
The accuracy can depend on projection type, but it is generally high in the central area of the projection (possibly lower for CassiniSoldnerProjection and LabordeObliqueMercatorProjection). In areas where the projection is very distorted, the accuracy can be worse. However, there should be no accuracy loss at the interrupted meridian of a regular cylindrical projection like LongLat or Mercator.
Output range
When p is sensible (inside the projection boundary and not at a pole), the result of the method will be normalized so that 0° ≤ result < 360°.
Platforms
Windows, Linux, Android